A Detailed and Understandable Explanation of Machine Learning
Posted in machine learning -
In recent years, the “hot” keywords: Machine Learning, Artificial Intelligence (AI), Deep Learning (Neural Network), etc. have become familiar with most of us. We hear about them all the time, from everywhere, but that doesn’t mean everyone understands them correctly.
By the mere meaning of the words, most of us can come up with understanding “Machine Learning” as make the computers learn. That is, more or less, a true point, but that creates more illusions than it helps clear. Are the computers really that smart, that they can learn things the way we, as human, learn? What if they learn so much, and start to have some consciousness of their own? Will we have a robots’ uprising someday? (Many of my facebook friends expressed that they’re scared computers will overcome us soon after reading Dan Brown’s Origin novel)
In this post, we will start exploring this mystery of artificial intelligence, by understanding what “Machine Learning” means. You aren’t supposed to become a ML expert (yet) after reading this post, but I bet you will have a much better understanding about this trending idea.
Definition
When programmers make a (normal) computer application, they will have to provide the computer the exact process (functions) and necessary parameters, and also cover all the possible scenarios that may happen in real life.
Suppose you are programming a program that plays chess, you will have to come up with every possible scenario of the board and prepare the equivalent reaction that the computer should do in each case. Not that it’s a very tedious (and impossible) job to prepare for every move in about 10^120 different games, you will also have to be a chess world champion to provide the exact move that the computer needs to make in each of those scenarios.
Even if for some reason, you were able to do that, there’s one more issue: at some point, there might be someone better than you in chess, and hence they can come up with better strategies than you did. As a human, you can quickly learn from them and adapt your strategy, but how will you give that to the computer?
Turns out, expressively program every possible scenario, in this case, is the wrong way to handle the problem. What we can do instead is to somehow provide the computer a “guideline”, from which it can generate an output based on any input. This approach has two advantages comparing to the previous one:
- The programmer doesn’t need to come up with a list of every possible move in every possible scenario, the computer will be the one that record new scenario when it sees one.
- As the computer exposes to more games, it can refine its strategy based on the input it receives (chess games from the past and maybe even in the future).
How do computers “learn”?
To better imagine how “learning” is for machines, let’s first talk about learning in human.
As human, we have several ways to learn: we can learn from someone else’s teaching, some someone else’ successes or failures, from books, and even from our own imagination, etc. Among the ways we use to learn, perhaps the most instinctive one, which we have done for millions of years and still continue doing today, is to learn by interacting with the environment, and earning feedback.
The basic idea of learning by interaction for human is to perform some action, receive a result, as well as a feedback for that result, based on which we adjust the action to try again, then receive the feedback and adjust the action, so on and so forth… until the feedback we get is “Correct” or we give up (It’s like joining “The price is right”, when you guess a price and the host says either “Lower” and “Higher” until your price is right, or you’re out of time and cannot guess more).
We also tend to generalize everything, so once we learn a lesson, the next time we see a problem with similar features (input) to what we have learned, we will tend to apply the same lesson to solve it. In the book Thinking, Fast and Slow, Daniel Kahneman expressed his idea of two “systems” inside our head, of which the first one is which acts on things fast and “automatic” based on what’s on the top of the head. The second system, which only enters when the first one gives up, will try to analyze the problem carefully, make more complicated considerations, etc. Since second system costs more energy and is (much) slower than the first one, so we tend to use the first system as much as possible: once a lesson is learned well enough (by the second system), it will be picked up by the first one, and become a sort of second nature to us. This can be seen quite clearly in sports: the athletes normally act very fast, even without thinking, due to their years of training, which transferred all solutions that they learned to their first systems.
If we apply Kahneman’s model to Machine Learning, we will see that machine also has two systems: one to “learn” (system 1) and one to act on new problems using what was learned (system 2), of which the system 2 is much more computationally costly. When a computer “learns”, it follows more or less the same steps as human:
- Start with some rough strategy and generate output with it.
- Get feedback
- Improve the algorithms to generate better results
- Get feedback again
- …
Some basic terms
The Learning Model
Earlier we have said that in order for the computer to “learn”, we need to give it some “guideline”, from which it can refine and improve by the inputs it receives. Since the computer is not human, the “guideline” needs to be very precise: the computer needs to know what are the things it’s supposed to refine, and how. Naturally, when it comes to preciseness and computers, one of the best tools that human has is Mathematical functions, and that’s what used in building machine learning algorithms.
By applying “an algorithm” to a machine learning agent, we apply one mathematical function, or a combination of mathematical functions onto the data, and the way computers refine and improve that algorithm is via changing the parameters of that function. Just as the algorithms used in a normaly software, a machine learning algorithm is also decided beforehands: only the parameters will be changing during the learning (training) phase.
Types of Machine Learning
Machine Learning, like many other complicated field, has several ways to clusify into categories, but perhaps the most widely-used method to divine Machine Learning is by their types of outcome:
-
Supervised Learning is the learning method in which the computer is provided data in the form of (input, output), i.e. for every input in the dataset, there is an observed output. The machine learning algorithm is normally expected to infer the relationship between the observed input and output, so that it can predict the output for new input whose output is unknown.
-
Unsupervised Learning is the type of learning whose data has only input (and no output). The purpose of the learning is to classify the inputs into (unnamed) groups, so that the difference between data points inside a group is minimized, and difference between data points in different groups is maximized.
-
Reinforcement Learning is the type of learning in which an agent interacts with an environment and is rewarded for “good” behavior and/or punished for bad ones.
I have found this image from cognub.com, which illustrates well the three categories and some of their applications.
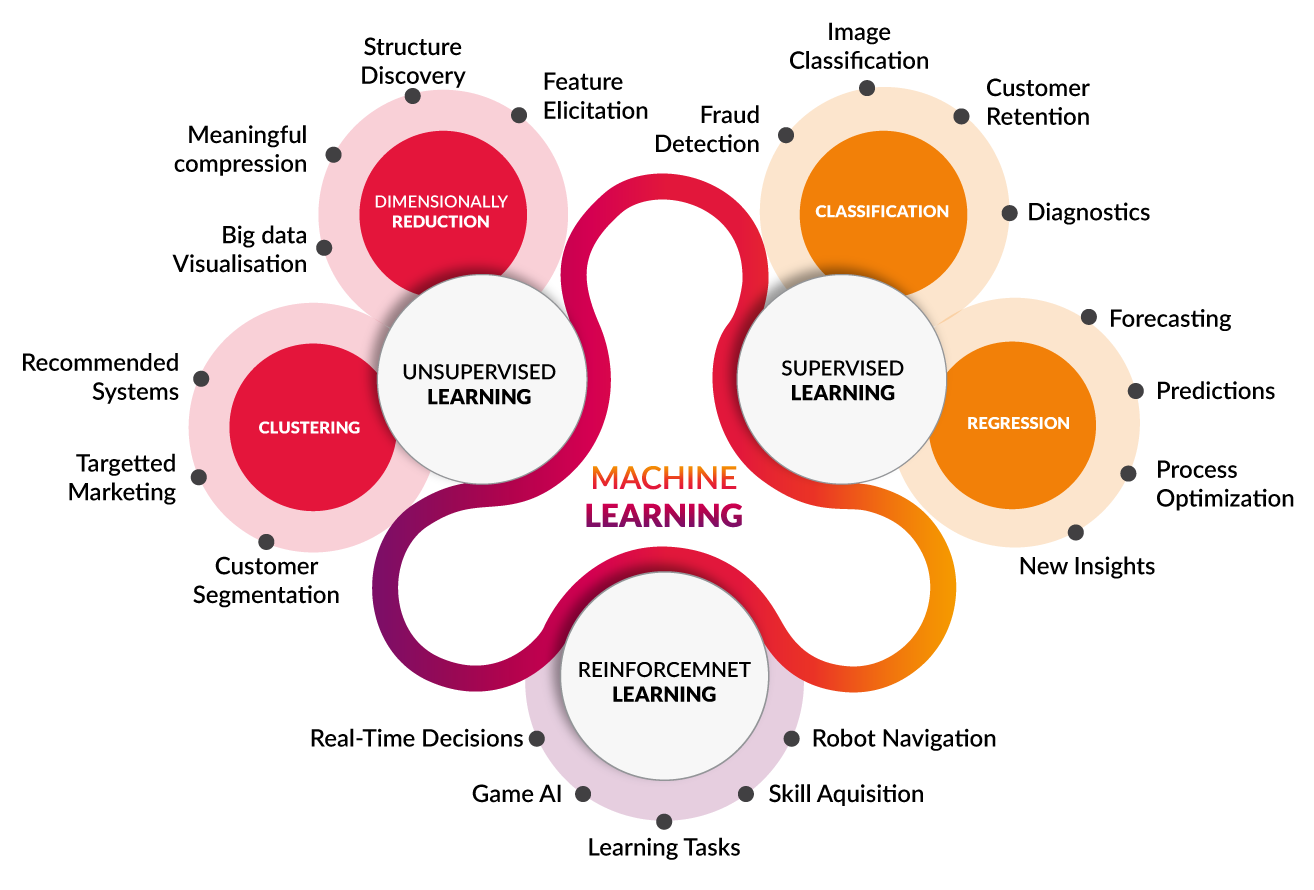
Branches of Machine Learning. Source: cognub.com
Cost Functions
As we talked earlier, a machine learning process normally starts with a pre-defined algorithm, which consists of one of more mathematical functions. The parameters of those functions are roughly guessed and/or randomly generated at first, from which the outcome is generated, and the feedback is used to refine the parameters.
Cost Functions is a way to measure the performance of the algorithm, and the mean for us to control the refinement of the parameters. Instead of asking the computers to “learn” (which basically means nothing to them), we program the computer to either maximized or minimized the cost function (if you recall your Calculus class, maximizing and minimizing functions are very suitable tasks for computers).
- In Supervised Learning, the “feedback” for current values of parameters are normally the difference (or deviation) of the outcomes calculated by the model (expected values) and the real outcomes (observed values). As this deviation is minimized, the similarity of expected values and observed values is maximized.
- In Unsupervised Learning, the concept of cost function is quite straight-forward: it’s simply a combination of difference among data points in one group (which needs to be minimized) and the difference among data points in different groups (which needs to be maximized).
- In Reinforcement Learning, we simply want to maximize the rewards and/or minimize the punishments.
Gradient Descent
In those machine learning algorithms that take into use minimization or maximization of functions, gradient descent is a method that is widely used. Simply put, it’s the same method that your Calculus teacher taught you back when you were learning how to find the minimum or maximum point in a function: by using derivative of the function. Recall that the cost functions is calculates the difference between real value and expected value, and that expected value is simply the learning model applied on the data input, the cost function is actually a function whose variables are the learning model parameters. We can, in theory, find a minimum in 2-D, i.e. when we have only one parameter to tinker).
When the number of parameters is larger than 1, things get more complex: while we can still get derivative of the function on each of its variables, we no longer can find the minimum immediately as in the 1-variable case. However, the sign of the derivative at least tells us that, as each of the variables increases while the others hold still, whether the function will increase or decrease, which in turns tells us whether we should increase or decrease each of the variables to go to a minimum/maximum point. From that point, for each of the parameters (cost function’s variables), we either increase or decrease it for some amount, and repeat the whole process to determine again if we have come to the point we want.
The amount that we either increase or decrease in each iteration is called learning rate, or alpha. Choosing a suitable alpha is also a hard job: a too big alpha can be dangerous as we may jump pass the optimum point repeatedly without ever reaching it, while a too small alpha may take forever to get to an optima, and we face the risk of being stuck in a local optima instead of going to the global optima, which we desire.
Overfitting/Underfitting
In Supervised Learning, we normally hear about the terms overfit and underfit. Those terms are actually quite self-explanable:
- Underfitting means the expected values generated by the model is too different from the observed (real) values. (i.e. the result of the Cost Function is not as good as the minimum acceptance).
- Overfitting means the opposite.
Wait, opposite? Like the result of cost function is too low?
Yes. Though it may sound a bit unreal (at first), there is a problem when the expected values are too closed to the real ones. In that case, the model is affected too much by the data we have in hands, which makes it less general for new data (i.e. if we use the model to predict new data, the result might be wrong since the model only works well with the data it used in training).
To prevent overfitting, in supervised learning, the data is normally divided into 2-3 groups, of which a big group of data is used for training the data (i.e. generating the parameters), while another group is used for validating the trained model, by applying the model on the input and calculating the cost function. The idea here is: since the validation data was not used in training the model, if the model can perform well on this group of data, it will be likely to also perform well on new data.
Only when both the train group and validation group of data result good (enough) result, then the model is said to be neither overfit nor underfit. Normally the training process will stop here, at which point an optional third group of data can be used to test the model a final time. As the test results of both train group and validation group of data is used to determine if we should stop the training, they are sometimes called the stop condition of the the model.
Q: Why do we need a third group of data to test? Is it a waste?
A: Though the validation data group was technically not used in training process, it was used to test the model repeatedly during the training, and contributes to at least half of the stop condition of the training process; for that reason, many researchers prefer to have a third dataset, something the model absolutely has never seen before to test it one last time. Whether or not this third group is required depends on the problem, your requirements and how much data you have.
The Process
With the newly acquired terms, we can describe a full machine learning process for a supervised algorithm as follow:
- We (human) decides which algorithm to use based on the problem and the amount of data we have.
- We divine the dataset into 2-3 groups, with the biggest group for training the model, and one or two smaller group for validation.
- The model is set up with some roughly guessed parameters.
- Perform the cost functions on the training set and validation test.
- Based on the cost function results, the parameters are adjusted (by using gradient descent for training set).
- Repeat step 4-5 a few times, until the results we get is good enough.
- (Optional) Test the model a final time with the test dataset.
Of course, following these steps doesn’t guarantee that you will get a state-of-the-art machine learning model. Since we always have to assume that the data follows some pre-defined equation, things get ugly frequently and it’s not uncommon to have to try several times to finally find a suitable model for the data. The lack of data is also a big problem, as no matter how “good” a model is, we can never train it well enough with not enough data. On the other hand, too much data has big hardware requirements, hence it’s very costly to do machine learning.
“A machine learning model is only as good as the data it is fed.” - A phrase that is quoted by so many people that I can’t verify who was the first one that said it.
I hope that this post helps you understand, at least, some basic concepts of Machine Learning, and clears the foggy ideas about its magic. If you would like to hear more about this topic, and/or some hands-on examples, please drop me an email to me@huymai.fi. See you next time!
